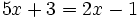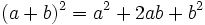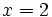Función lineal
Introducción: Recordemos que una función es una correspondencia entre los elementos de un conjunto de partida, llamado Dominio, y los elementos de un conjunto de llegada, llamado Codominio, de forma tal que a cada elemento del dominio le corresponde uno, y solo uno, en el codominio.
Definición: Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio son también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.
Definición f: R —> R / f(x) = a.x+b donde a y b son números reales, es una función lineal.
Este último renglón se lee: f de R en R tal que f de equis es igual a a.x+b
Por ejemplo, son funciones lineales f: f(x) = 2x+5 , g: g(x) = -3x+7, h: h(x) = 4
Definición: Las funciones lineales son polinomios de primer grado. ver grafica ejes Recordemos que los polinomios de primer grado tienen la variable elevada al exponente 1. Es habitual no escribir el exponente cuando este es 1.
Ejemplos de funciones lineales: a(x) = 2x+7 b(x) = -4x+3 f(x) = 2x + 5 + 7x - 3
De estas funciones, vemos que la f no está reducida y ordenada como las demás. Podemos reducir términos semejantes para que la expresión quede de una forma mas sencilla, f(x) = 9x + 2
Tambien recordemos que hemos convenido que cuando no establecemos en forma explicita el dominio y el codominio de una función, supondremos que es el mayor conjunto posible en cada caso.
Por ejemplo, si hablamos de la función f, de dominio real y codominio real, tal que f(x)= 2x-6, anotaremos f: R ——-> R / f(x) = 2x-6 Siendo el dominio todos los números reales, R, y el codominio también, todos los números reales, R.
Esto se lee " f de R en R tal que f de x es igual a 2x-6"
Vamos a graficar esta función, que tal cual lo vimos en la definición, es una función lineal por ser de primer grado. Para graficarla haremos una tabla de valores.
f: R ——> R / f(x) = 2x-6
Le vamos dando valores a "x". ¿Que valores le podemos dar? Cualquiera que este dentro del dominio.
Por ejemplo, si x = 5 , entonces f(x) pasa a ser f(5), que es f(5) = 2.(5)-6 f(5) = 4
Entonces al 5 le corresponde el 4. Nuestro punto es el (5,4).
¿Cómo se coloca en un par de ejes coordenados? ¿Que tal si repasamos esto?
Y ahora que ya sabemos colocar los puntos, podemos hacer la gráfica de una función lineal. Con el botón "paso a paso" iremos construyendo juntos la gráfica de una recta. Cuando termines, con el botón "de nuevo" podrás hacer otra gráfica.
f: R —> R / f(x) = a.x+b
Una función lineal cumple además, que el incremento de los valores de los elementos del dominio es proporcional al incremento de los valores en el codominio, siempre que a no sea cero.
Este número a se llama pendiente o coeficiente angular de la recta.
Volvamos a esto ejemplos de funciones lineales f: f(x) = 2x+5 , g: g(x) = -3x+7, h: h(x) = 4
f: f(x) = 2x+5 si x es 3, entonces f(3) = 2.3+5 = 11
si x es 4, entonces f(4) = 2.4+5 = 13
si x es 5, entonces f(5) = 2.5+5 = 15
Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, f(x), se incrementa en 2 unidades.
Preste atención en que los valores de x y de f(x) NO SON PROPORCIONALES.
Lo que son proporcionales son los incrementos.
g: g(x) = -3x+7 si x= 0, entonces g(0) = -3.(0) +7 = 0+7 = 7
si x= 1, entonces g(1) = -3.(1) +7 = -3+7 = 4
si x= 2, entonces g(2) = -3.(2) +7 = -6+7 = 1
Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, g(x), disminuye en 3 unidades.
h: h(x) = 4 si x= 0 , entonces h(0) = 4
si x= 98 , entonces h(98) = 4
Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, h(x), NO aumenta. Es la función constante. Su gráfica es una recta paralela al eje OX.
¿Que diferencia fundamental y muy importante hay entre las funciones h y j?
Parecería, a primera vista, que son muy parecidas. Las "fórmulas" de ambas son iguales. h(x)=3 y j(x)=3
Sin embargo, son muy distintas porque mientras la función h tiene como dominio todos los números reales, la función j tiene como dominio los números naturales. Y como entre dos números naturales consecutivos no hay ningún otro número natural, no existe gráfica ni puntos entre ellos.
Esto es, entre el 17 y el 18 no hay ningún número natural. Entre el 17 y el 18 hay infinitos número reales. He ahí la diferencia.
La representación gráfica de h es una linea recta, pero la de j son puntos aislados, aunque son infinitos.
Esto, por supuesto, ocurre no solo si son funciones constantes. Es para cualquier función. El dominio es muy importante. Cuando no se especifíca el dominio y codominio, se supone que son los mayores posibles. En el caso de las funciones lineales, es de R en R.
Veamos otro ejemplo: 
Esta función, llamada q, ¿ será lineal ? Supongamos, además, que es una función de R en R.
Para determinar esto tenemos que ver si las diferencias entre los valores en el dominio y codominio son proporcionales. Esto es, si cambian en la misma razón.

 se llama ecuación.
se llama ecuación. 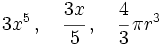
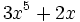 (binomio),
(binomio), 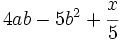 (trinomio)
(trinomio)